Loop antennae have been used from ELF to UHF since the beginning of radiocommunications. At low frequencies, the main problem for loop antennae is to have enough sensitivity; the antenna being very small respect to the wavelength the collected energy is also small. To increase the output level the loop may be made resonant, so loosing itís intrinsic aperiodic characteristics.
Being interested in monitoring the ELF/VLF spectrum I started thinking about loop physics. My goal was to have reproducibility between different monitoring stations, so to be able to quantify the measured signals. This is not so easy, since the overall gain of the various loop/preamplifier combinations is not known; also, the frequency response is often far from flatness.
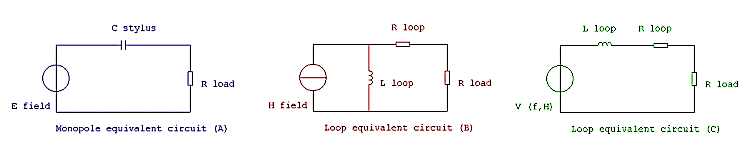
A small diameter loop is the electric dual of a short monopole antenna, which is a well-known object. A monopole loaded by high resistance goes easily down in frequency: itís quite easy to monitor the atmospheric electricity by connecting a high-Z preamplifier to a vertical antenna (ask Mr. Benjamin Franklin!).
The loop preamplifiers used in many designs also are high-impedance devices. This sounded wrong to me - if the monopole is high-Z, the loop should be a low-Z generator.
So I started writing a table with the dualities and correspondent characteristics of the two. Some "strange" statement will be explained later.
DUALITY
| Short monopole | Small loop |
| Sensitive to electric component of the field (E) | Sensitive to magnetic component of the field (H) |
| Output voltage proportional to E field | Output current proportional to H field |
| Output voltage independent from f | Output current independent from f |
| Equivalent circuit: a voltage generator (the E field) in series with a capacitance (intrinsic capacitance of the stylus to ground). The load resistance forms an high-pass filter with the capacitance (see fig. 1A) | Equivalent circuit: a current generator (the H field) in parallel to an inductance (intrinsic inductance of the loop itself). The load resistance (in parallel to the inductance) forms a high-pass filter with the inductance. The wire resistance (Rloop) is in series with the load resistance, effectively limiting the output current (see fig. 1B) |
| The load should have an infinite resistance to have a flat response at f=0 | The load (including Rloop) should have a zero resistance (infinite conductance) to have a flat response at f=0 |
| The E field is not perturbed by the monopole (no current flowing) | The H field is completely reflected by the loop (the current flowing into the loop is of opposite sign respect to the incoming field, and tends to cancel the field, so reflecting the incoming wave) (Note 1) |

Now, back to some maths (thanks to Will Payne, N4YWK, for loop theory).
The electrical model of a loop antenna (fig. 1B) may be transformed in a voltage generator (the open-circuit voltage described in (1)) in series with an inductance and a resistance (fig. 1C). Note that the generatorís voltage is now dependent from F.
The L is the intrinsic inductance of the loop; the R is the resistance of the loopís wire.
Open circuit voltage of a multi-turn loop is defined as:
![]()
Where:
2pm0is
a constant. m0equals
4p10-7
N, number of turns
A, loop area in m2
H0, applied magnetic field
in ampere/meter
f, frequency, in Hz
cosq,
cosine
of angle between loop axis and field vector, assumed equal to 1 (optimal
orientation)
Consider now a loop closed on a zero impedance, or short-circuited. The current flowing in the short is:
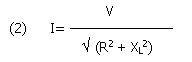
Where V is the open circuit voltage, R is the conductor resistance and XL is the loop reactance, so XL =2p f L. Let define Ö (R2 + XL2) as Zloop, it will be useful for noise calculations.
Developing and rearranging terms of (2) we have:
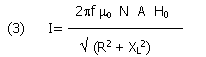
This equation is very interesting, since it shows that for small values of f the output current is limited only by R and increases with f; when XL becomes bigger than R the output current is limited mainly by XL and is no more dependent from f!
(To be correct, R is not strictly frequency independent due to the "skin effect" and distributed capacitance at higher frequencies. We may ignore this effect if we stay under Ė say Ė 20% of the self resonant frequency of the loop Ė more later)
So if we want a flat frequency response from a loop the best way is to close it in short circuit, and use the output current instead of voltage. This will be the best way to extract the signal from the antenna.
We may now define a low frequency cutoff for a shorted loop. For frequencies larger than
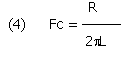
The output current tends to be not function of f; below this value we have a 6dB/octave rolloff.
(More correctly: with reference to eq. 3, we can ignore R, when R2 is, at least, an order of magnitude smaller than XL2. Conversely we could ignore XL when XL2 is an order of magnitude less than R2).
For any loop geometry and number of turns, the Fc may only be lowered lowering R, since L is fixed. Our ideal loop would be a superconductive one, and people working with NMR and magnetometers knows it well. Unfortunately a cryogenic loop is not in my budget - but it will have, and has, full flat response down to zero Hz (Note 1).
So we may draw a diagram like this:
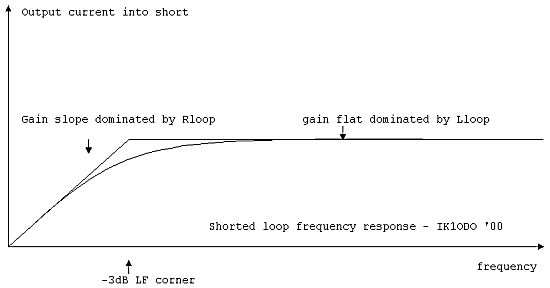
The frequency response behavior is evident. At low frequencies the output current increases with f, then the reactance prevails and the frequency response flattens.
[Incidentally, resonating a loop with a capacitor in series equals to cancel out the series L; the gain obtainable resonating a loop is proportional to the inverse of Rloop. This is only a different way to define Q, always equal to XL/RS].
So I started designing single-turn loops coupled to a current-to-voltage converter, like this:
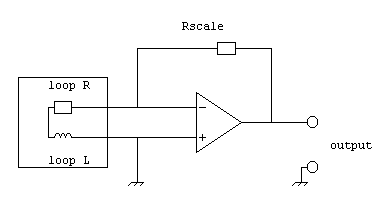
The output voltage is, simply, the loop current multiplied by Rscale. The loop is closed into the "virtual ground" created at the input of the op-amp. The circuit works, but isnít so easy to implement. The main problem is to keep Rscale over 200 Ohm, which is the minimum impedance that a typical low noise op-amp like the OP27 may drive. If the loop R is small the DC gain becomes enormous. To give an example, a single 1m loop made of 5/8" semirigid coax cable has an R of 50 mW, L is 3 mH, and so Fc is around 2,7 kHz. Using the minimum value of 200W for Rscale the DC gain is about 4000, and this poses problems on the gain-bw product of the op-amp (Note 2).
A big advantage of such a circuit is that the loop is grounded, and the common mode signal impedance is very low; screening the loop is really not necessary, so itís easier to build (Note 3).
Running the loop into the virtual ground at the summing node, the distributed capacitance of the loop has no effect on the output, since there is no voltage between adjacent turns. This means no resonant behavior (within the limits of the opampís slew rate ability to maintain the virtual ground). The immunity to stray capacitance also means less coupling with nearby objects. The behavior of the loop is completely predictable, and the frequency response is flat over many octaves, even if the loop is wound randomly (basket-weave windings are needed to reduce stray capacitance and maximize output voltage in resonant loops, and is not needed here. Less elegance in the loop, more elegance in the preamplifier...)
Results on paper and circuital simulations were encouraging, so I started thinking of bulk copper loops Ö milliohm resistance, and big difficulties in the amplifier. A 2m single turn made by half-inch copper pipe may have 35 mm2 section, 6 mH inductance and only 3 mW resistance, giving a low frequency corner at 90 Hz! But the amplifier would have to source hundreds of mA to compensate the input DC offset, and becomes impractical.
A way to overcome this is again to use many turns, but keeping the section constant.
If our 35 mm2 copper pipe is divided into 10 conductors of 3.5 mm2 each we have:
- 100 times the inductance (proportional to the number of turns squared)
- 100 times the resistance (one tenth the section, ten times the length)
and the same cutoff frequency! (R/2pL)
So, the rule is: in this circuit, given a loop diameter and geometry the only way to increase the sensitivity to low frequencies and lower the natural cutoff frequency of the loop is to have more copper weight. The number of turns seems not really that important, and the resulting sensitivity is determined by the op-amp gain.
SYSTEM CALIBRATION
Now, it would be nice to know the output voltage for a known H field, that is, the transducer gain of the loop. Returning to equation (3):
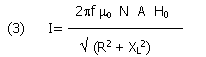
For f>>fc it may be simplified and we have:
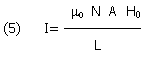
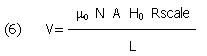
The transducer gain, H field to output V, is:
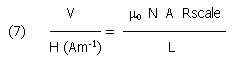
Therefore
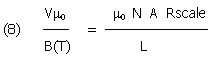
Or, if you want to read magnetic field in picoTesla - pT (and cancelling m)
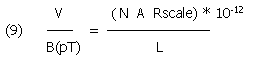
This allows us to calibrate the system. Let assume the following parameters:
Our 100 turn, one meter loop of 1.75 mm2 wire has A=0,785 m2. The copper wire resistance is 19 mW/m/mm2, so we have about 3.5 W for 315m. The inductance is 20 mH, giving an Fc of 28 Hz.
A reasonable Rscale may be 20.4 kW, so we have G=100 V/ Am-1 or 0,26 V/Vm-1. The field intensities in this part of the spectrum are quite high, and a gain like this should be enough.
If we want to calculate the gain in V/pT, we get 80 mV/pT.
NOISE CONSIDERATIONS
The ultimate sensitivity in such a system will be limited by noise in the op-amp. The best low-noise audio op-amps (like AD797 from Analog Devices or the LT1028 family from Linear Technology) have about 1 nV/Ö(Hz) equivalent input noise voltage density. The op-amps also have an associated noise current, but the noise voltage is the predominant source in our application. This noise appears as a voltage generator in series to the op-amp input, is directly amplified by the ratio Rscale/Zloop and appears at the output Since Zloop changes with F, the noise also changes, being maximum below Fc.
The noise equivalent circuit is:
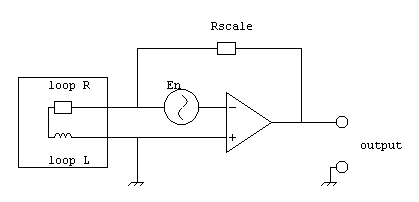
The noise voltage causes a noise current to flow into the loop:
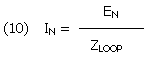
And the from eq. 7 the equivalent noise magnetic field seen by the circuit is:
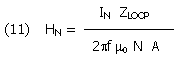
Substituting eq. (10) for IN we obtain the noise floor equation for our circuit:
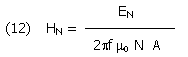
Where EN is the equivalent noise voltage density of the op-amp, usually expressed in nV/Hz-1/2, and HN is the noise floor of the antenna system, expressed in nA/ Hz-1/2.
And giving it in pT:
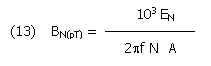
The last two equations are the kernel of the problem. To obtain maximum sensitivity and low noise we need low noise op-amp, many turns, large aperture, or high mu; all the remaining parameter just do disappear.
And to obtain a good response at low frequencies we need low R, so thick wire.
With our sample loop of 1m, 100 turns, the ultimate noise floor will be about 1.6 nAm-1Hz-1/2 at 1 kHz, and 160 nAm-1Hz-1/2 at 10 Hz; or 0.6 and 60 mVm-1Hz-1/2; or 0.002 and 0.2 pTHz-1/2.
Not so bad for an antenna of only 1 m! For comparison, the intensity of the first Schumann resonance at 7.8 Hz is around 1 pT.
THE FINAL CIRCUIT
A version of the circuit has been tested by Renato IK1QFK, and is described on his web site http://www.vlf.it
A possible VLF/ELF loop (my Ideal Loop!), going down to the Hz domain, and still easily buildable, may have the following parameters:
- 1m diameter loop, unscreened, made by 100 turns of 1.75 mm2 wire. This means a total section of 175 mm2, a resistance of 3.5W, an inductance of 20 mH, and a cutoff frequency of about 28 Hz.
- the amplifier should have an Rscale around 20kW, and the IC is a low noise device like AD797 or LT1028. No more components are needed - only a potentiometer to balance the offset! (This is the simplest loop preamplifier ever seen). You may have to add some capacitors, like Renato did, to stop MF interference, and a C in parallel to Rscale for the same purpose. I am currently experimenting with a practical design like the following:
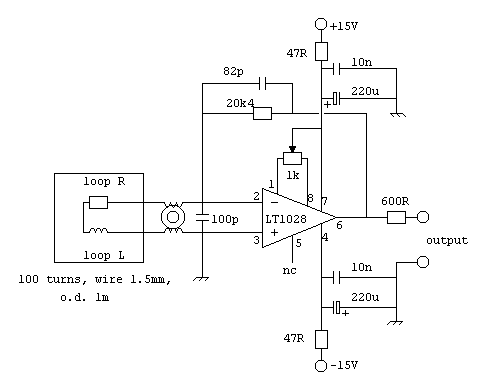
Circuit description
The loop is connected to the LT1028 (or LT1028A, or AD797) low noise op-amp. The amplifier acts as current to voltage converter. The DC gain is set by the ratio Rscale (20k) / Rloop (about 3.5 Ohm). The toroid is wound as common-mode current choke, to stop HF signals coming from the loop. The capacitor in parallel to the input has the same purpose.
The 82pF cap in parallel to Rscale limits the high frequency response to about 100 kHz, since Iím not interested in higher frequencies. The 600W resistor in output matches the preamp to a shielded microphonic cable (two pairs plus screen), one used for power supply, the other for the signal.
The power supply is decoupled close to the IC to improve noise rejection (the PSRR of those op-amps is not very high).
The offset nulling pot is a multi-turn miniature trimmer. The circuit connections are and values are for the OP27 and LT1028. If you use an AD797 the pot must be a 20 kW one, connected between pins 1 and 5, with the wiper connected to pin4 (-Vcc).
All resistors are metal layer, ¼ W, 1%. Precision metal layer resistors are less noisy than the usual carbon types. Small capacitors are polystyrene or Mylar. The input choke is wound as 5+5 bifilar turns over a 1-inch high permeability toroid, used for noise suppression. Use thick wire (at least 14AWG or 1mm); this choke is non critical, but his resistance is a true parasite parameter in series to the loop R.
The preamplifier is mounted inside a metal box close to the loop. After power up allow some minutes for thermal stabilization, then turn the potentiometer for zero output DC level. It may be necessary to readjust the offset after one month of continuous operation; the op-amp has to season.
You need about 320m of wire to test the design, and a solid form (octagonal or circular) to wind it up. The total wire weight is about 5 kg for 100 turns on 1m dia. If you donít care about high frequency performance of the loop (over 1 MHz, I mean) the turns may be close wound. I used 1.5 mm (60 mils) dia wire, enamel coated.
Results are impressive Ö the antenna has essentially flat frequency response from 30Hz to 1 MHz, over four and half decades, and is useable down to 10 Hz. The noise is so low that you may use it for nature radio monitoring, down to Schuman resonances in 7-50 Hz band.
CONCLUSIONS
A comparative discussion about optimal loading of loop antennae demonstrates the advantages of a current-mode loop.
A current-to-voltage converter loop preamplifier has been described and analyzed. In particular, the sensitivity parameters have been derived to allow comparative monitoring of ELF/VLF/LF signals.
The noise contribution of the op-amp in the preamplifier has been calculated, and guidelines for optimal noise performance have been described.
A practical and reproducible design is presented, allowing monitoring of ELF/VLF/LF spectrum with small area loops.
THANKS to:
Notes:
(*) Marco Bruno, IK1ODO. E-mail: IK1ODO@libero.it .
The author reserves the copyrights
on this work. The circuits may be reproduced for amateur purposes. The
article or parts of it may be reproduced indicating the source.
 |
(1) Have you seen the
small magnet floating over a superconductive disc (photo copyright by Edmund
Scientific)?
Well, the magnet is a DC signal, a steady magnetic field, and the disc is a shorted loop of zero resistance Ö a current flows in the loop, perfectly mirroring the field of the magnet, which is reflected! |
(2) Any operational amplifier has a fine gain-bandwidth product; for the OP27 it is 8 MHz, for the AD797 100 MHz. Please refer to the producer data sheets for definitions. The meaning is that with an OP27 we may have a voltage gain of 1000 up to 8 kHz, or a gain of 100 up to 80 kHz. The circuit designer should avoid approaching this limit.
(3) The sensitivity of loops to E fields has been discussed several times. The E field may appear as a common-mode voltage at the terminals of a floating loop (in other words, the voltage is the same between each terminal and ground, and there is no voltage difference between loop terminals. To exclude this kind of signals loops have been screened; but screening has the adverse effect to increase distributed capacitances and lowering the maximum useable frequency of the loop.
In this design the loop has an intrinsic low impedance, and common mode voltages are ignored by the op-amp, so screening is really not necessary; also, stray capacitance is ignored, since there is no voltage difference between turns, so no current in the associated capacitance.