PDF version of this article is available here

ON THE POSSIBLE ORIGIN, PROPAGATION AND DETECTABILITY OF ELECTROMAGNETIC PRECURSORS OF EARTHQUAKES

E. R. Mognaschi, IW2GOO

Dipartimento di Fisica "A. Volta", Università di Pavia, via A. Bassi 6, I-27100 Pavia, Italy and Istituto Nazionale di Fisica della Materia, Unità di Pavia

Some mechanisms on the origin of electromagnetic precursors, expected to be generated well before the occurrence of an earthquake, due to the process of rocks microfracture, are presented and discussed. The wide frequency spectrum of electromagnetic signals produced by the damped dipole oscillations caused by the microfracture process is described. The propagation of low frequency electromagnetic waves in the ELF and ULF range, belonging to such spectrum, is studied with reference to the electrical properties of rocks constituting the lithosphere. The characteristics and the possible propagation paths of such waves, both underground and over the Earth surface, are considered. A method based on the delay of reception between slow underground electromagnetic waves and waves which travel in the atmosphere at about the light speed is proposed in order to estimate the distance of the source of electromagnetic precursors from the observing station and, hence, to locate the source by means of a network of stations.
 
 

1. INTRODUCTION

The occurrence of earthquakes is associated with the release, in a short time interval, of a large quantity of energy coming from a confined volume below the Earth surface.

The linear dimensions of the focal region in most earthquakes is of the order of few kilometres or even less, while, in large magnitude earthquakes, may be greater. The focal region may be approximated, for the purposes of the present work, to a source of spherical waves or of cylindrical waves if one of the dimensions predominates over the others. The centre of the focal region, referred to as the focus, is normally, for shallow shocks, at depths less than 60 km which is about only 1% of the Earth radius, although a small number of earthquakes have greater focal depths. This is in agreement with the consideration that most ordinary earthquakes appear to be originated above the Mohorovicic discontinuity, which is placed at depths from about 30 to 60 km. Intermediate shocks originate at depths between 60 and 300 km, while deep shocks originate at depths greater than 300 km, with a maximum depth recorded of about 720 km. While deep and intermediate shocks are limited to the circum-Pacific belt and to the trans-Asiatic belt (Gutenberg, 1954), the region which extends from Asia Minor to Italy, is usually interested mainly by shallow shocks; besides, strong earthquakes are observed in the subduction region of the Hellenic arc.

The purposes of the present paper are: i) to discuss an hypothesis on the possible mechanisms which could give rise to electromagnetic waves from the focal region well before the appearance of shock waves, ii) to describe the propagation of such waves in the Earth crust and their refraction through the Earth/atmosphere boundary and, finally, iii) to estimate the detectability of such waves with the aim of proposing their use to determine the location and, possibly, the magnitude of impending earthquakes.

2. ENERGY RELEASED IN AN EARTHQUAKE

The energy of an elastic wave of given frequency is proportional to the square of the amplitude. Then, different earthquakes at a fixed distance should have energy proportional to the square of the recorded magnitude. For various reasons such a crude model does not fit the experimental observations and an empirical relation has been found between the magnitude of an earthquake and the total amount of energy released in which the exponent is somewhat less than 2. The energy E, corresponding to a magnitude M from body waves has been found to follow, to a first approximation, the law

log E = 5.24 + 1.44 M         (1)

where E is measured in joules (Båth, 1973). Notice that eq. (1) is valid only for M > 5 and should not be used for lower magnitudes. A magnitude increase of one unit in the M-scale corresponds to an energy increase by about 27 times. For M = 7 eq. (1) gives E » 2 ´ 10¹⁵ J and, for M = 5, E » 3 ´ 10¹² J. For smaller magnitudes, although an analytical expression is not available, the energy released is obviously smaller, but nevertheless very large. Such enormous energy amounts are accumulated, before an earthquake, in the Earth’s crust geological structures during time intervals which are often very long as compared to the human time scale, and stored as elastic energy associated with the compression and deformation of rocks. This mechanical energy is then released mainly in the short time during which the largest shocks are produced, but part of it is spent in the microfracturing processes of rocks before the rocks failure. In this work we are interested in the various mechanisms and phenomena which precede the earthquake itself, which could be useful as precursors signals of an impending earthquake. To this purpose, since it is very difficult if not impossible to gain a direct knowledge of the rocks behaviour under the real conditions in the Earth crust, we will refer to laboratory experiments on the compression of rocks and, from them, we will infer their behaviour in the Earth crust, being well aware of the differences of conditions between the two cases mainly as concerns the temperature and the water content of rocks and the way in which stresses are applied. Rocks temperatures are usually higher in the Earth crust than in laboratory experiments; the water content is greatly influenced by the environmental conditions such as pressure; when rocks are machined to a various degree, at atmospheric pressure, for laboratory tests they are, consequently, more or less dehydrated; stresses can be applied in every direction in the Earth crust, while in many laboratory tests, for convenience, only uniaxial stresses are applied to rock samples. Finally, in laboratory tests, simulation of tectonic conditions by applying stresses at a convenient slow rate is not always possible. Nevertheless, with due limitations, the overall behaviour of rocks in the Earth crust can be deduced from laboratory experiments.

3. ROCKS FRACTURE

The successive stages which lead to fracture of brittle materials, such as rocks, are the following: i) accumulation of stress; ii) microfracturing; iii) dilatancy; iv) macroscopic breaking. This last stage, connected with the sudden stress drop, leads to the crumbling of the sample in laboratory tests; while, in the Earth crust, gives origin to seismic waves. The applied compressive stress for which fracture occurs in laboratory experiments depends on the speed at which the stress increases, on the previous history of the samples and, of course, on the kind of rock considered. For granite, e.g., a typical value is 2.3 ´ 10⁸ Pa (Reynolds, 1961), which is one of the highest values observed. This stress corresponds to an energy density U, stored in the sample before the fracture, of 2.3 ´ 10⁸ Jm-³. If we assume that the average value of bond energy u for a single atomic bond is about 2 eV, a rough estimate of the number N of atomic bonds per unit volume at the rock crumbling in laboratory experiments can be obtained as N = U/u » 7.2 ´ 10²⁶ m-³, which corresponds to about 3% of the total number of atomic bonds in the rock.

During stage i) the stress, usually, increases continuously in naturally occurring phenomena. This stage can last many years up to centuries, while in laboratory experiments its duration is determined by the experimental set up and it is, obviously, considerably shorter. As previously pointed out, the speed the applied stress grows is of relevance for the dynamics of fracture and even for the final value of stress which correspond to the macroscopic breaking.

The microfracturing stage is the most interesting one to the purpose of the present investigation. Measurements of wave velocity and electrical resistivity (Mogi, 1973) indicate the formation of open cracks, while various authors have detected acoustic and/or ultra-acoustic emissions during stage ii) (Scholz, 1968); measurements of crack velocity in norite (Bieniawski, 1967) showed that crack propagation starts with low velocity and grows up to the point in which the elastic energy released by crack development is insufficient to maintain crack propagation. This results in a rapid increase of crack velocity, until a terminal velocity is reached which is about one half of the shear wave velocity. The measurement of a terminal velocity of 1875 ms-¹ permits to evaluate the limit number n_L of cracking events per unit time. By assuming a lattice constant of a few Å the order of magnitude of n_L lies between 10¹² and 10¹³ s-¹. Both analytical and numerical solutions for the dynamics of earthquakes in model systems give a power law distribution for the number n of failure events, n being related to the released elastic earthquake energy E by a law of the type n ~ E-^c with c ~ 1. These models indicate that the empirical law (1) is due to the self-organised critical behaviour of earthquakes (Chakrabarti and Benguigui, 1997).

The crack propagation process generates elastic shock waves which travel in the rock. Detection of such waves permits the observation of microfracturing (Scholz, 1968). However, very little is known about the frequency spectrum of elastic shock waves produced during microfracturing except that the spectra are very wide and are characterised by a large amount of low frequencies (Mogi, 1973). The elastic shock activity depends also on the mechanical and structural inhomogeneities and it was found that the more heterogeneous the rock is, the greater is the elastic shock activity during compression (Mogi, 1973). The microfracturing stage is characterized also by a flurry of activity which occurs at low stresses; as stress increases, this activity, at first, slows down to a very low level, then begins to increase again at stress values which are approximately half the fracture stress. Its rate increases until just before fracture with a very rapid acceleration (Scholz, 1968). In a study of acoustic emissions from rapidly moving cracks in glass and polymethyl methacrylate (known as PMMA or Plexiglass or Perspex) (Gross, 1993) it was estimated that about 3% of the energy of an advancing crack is converted in acoustic emissions. In the present work we suppose that a fraction of the elastic energy stored in the rocks could be converted into electromagnetic energy, with mechanisms which will be discussed in the next section. Even if the fraction of energy were small and the radiation mechanism had small efficiency, it is estimated that an appreciable amount of electromagnetic energy could propagate towards the Earth surface and above it. This energy, in form of electromagnetic waves, as will be discussed below, could be detected as radio signals at the Earth surface.

Above about half the fracture strength the stress-strain curve is no more linear. This is the stress region in which dilatancy, iii) stage, occurs. In laboratory experiments dilatancy corresponds to an increase of volume of rocks, with increase of stress, due to the formation of new void space produced by cracking. In rocks of the Earth crust the dilatancy is accompanied by the flow of pore water in the dilated region with increase of internal pressure and reduction of internal friction and electrical resistivity.

4. GENERATION OF ELECTROMAGNETIC SIGNALS

Recently Mognaschi and Zezza (Mognaschi, 2000) observed that a possible mechanism for the generation of electromagnetic waves in the litosphere is to be identified with the microfracturing process of rocks. These microfractures, in turn, involve the breaking of a large number of atomic bonds, i.e. the covalent or ionic bonds giving rise to the crystalline structure of the rocks. The formation of unbalanced charge distributions, of opposite sign, on the opposite sides of the microfractures is to be expected and, consequently, the onset of strong local electric fields. The existence of such fields was demonstrated in experiments, performed under vacuum, on the breaking of adhesion bonds. Potential differences reaching 10⁴ V were estimated from the spectrum of X-rays emissions with a flux of 10⁹ photons cm-² (Klyuev, 1984).

In fracture experiments performed in air at atmospheric pressure, rocks usually contain microcavities with adsorbed gases, it is therefore possible that the breakdown voltage of the gases can be locally exceeded with consequent generation of micro electrical discharges and emission of electromagnetic waves.

Another mechanism has also been suggested (Mognaschi, 2000) which could be effective in the fracture of rocks which are poor conductors of electricity. The electric charges of opposite sign, created on opposite sides of microfractures, constitute electric dipoles which have a lifetime determined by the electrical relaxation time of the material. Such dipoles have a linear dimension corresponding to the width of the microfracture. This dimension can be modulated by the damped mechanical vibrations, originated by rupture of the atomic bonds, of its walls giving rise to dipole oscillations.

The electric relaxation time t of a material is given by the product of the resistivity r times the permittivity e , i.e.:

t = r e = r e_oe_r         (2)

where e_o is the vacuum permittivity and e_r the relative permittivity of the material. The values of e_r of rocks mainly lie in the range from about 4 to 16 for dry rocks and can reach values up to 50 in wet rocks, but values as high as 1000 are also reported (Parkomenko, 1967) for some minerals. Resistivity of rocks, on the contrary, varies over a range much wider than any other physical property. Values as low as 10² W m in wet rocks and as high as 10¹⁸ W m in some dry marbles are reported (Parkomenko, 1967). Relaxation times ranging from 0.1 s in limestone and dolomite and 0.8 s in glacial till are common values, although values short as 10-⁵ s can be estimated for wet gneiss (Parkomenko, 1967).

A relaxation time of tenths of seconds is sufficiently long to allow for the efficiency of the proposed mechanism based on the oscillation of the electric dipoles generated by the fracture process. Taking into account the crack dynamics, which involves a finite speed of propagation of cracks and crack branching, the number of dipoles generated should increase with time so that a very large number of dipoles, increasing with time, is expected to be present, even if each of them have a limited lifetime. During the fracture process mechanical vibrations, arising from the breaking of atomic bonds within the material, give origin to the well known mechanical damped acoustic and ultra-acoustic vibrations. Such vibrations can also produce oscillations of the electrical dipoles localised along the microfractures. The resulting damped electrical dipole oscillations will, in turn, give rise to electromagnetic waves.

In the case of rocks containing piezoelectric components, like e.g. quartz, electromagnetic emissions can be generated by the process of recombination of electric charges induced by stress release (Matsuda et al., 2001). This last mechanism could be active only in rocks containing a substantial amount of such components.

A model which takes into account the dislocation dynamics in the preseismic micro-crackings located in an earthquake preparation zone was recently developed (Teisseyre, 2002) to explain high noise levels in VLF and ULF bands frequently observed before earthquakes (Meloni et al., 2001).

Whatever the mechanism of generation of electromagnetic waves, our model consists of a large number of small electric dipoles whose linear dimensions d are those of the width of the fracture which perform damped oscillations. Electromagnetic emissions should start with the beginning of the microfracturing process, so that the number of dipoles involved should reach, at the end of the process, the number N of broken bonds. However, since not all the bonds are fractured simultaneously, the instantaneous number of broken bonds will depend on the dynamics of fracture and will be substantially lower than N.

An electric dipole of moment p = de, where e is the elementary electronic charge, performing damped oscillations with frequency n₀ = w₀ /2p and wavelength l₀, generates in a medium of permittivity e , magnetic permeability m @ m₀, at a distance r from the dipole, in the direction q with respect to the dipole axis, a magnetic field B given by (Stratton, 1941)

B(r, q , t) = Ö (m₀/e ) p/(2l₀) [i/r² - 2p /(l₀r)] sin q exp - i(w t - 2p r/l₀) exp (-g t).      (3)

Where g is the damping factor, where g ³ t-¹.

Eq. (3) can be rewritten in the simplified form

B(r, q, t) = A(r, q) cos (w_ot - 2p r/l_o) exp (-g t)         (4)

where A(r, q) is an amplitude factor which contains the 1/r² and 1/r behaviours of the field and its angular anisotropy.

The power spectral density S(w) of the wave (4) is given by (Stratronovic, 1963)

S(w) = 4g A(r, q) [w² + w_o² + g²]/[(w² - w_o² - g² )² + 4 g²w ²].         (5)

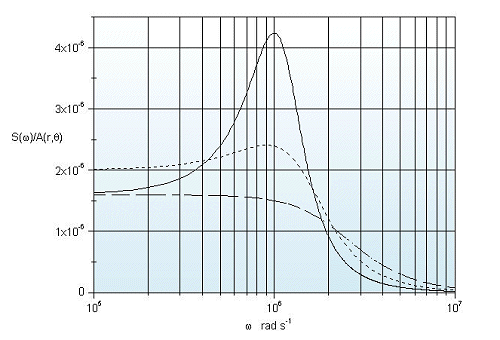
S(w) shows a broad maximum as near to w_o as smaller the damping factor g is. It is also relevant that it has non vanishing components at frequencies which are low with respect to w_o, i.e., for example, in the VLF region (30 kHz - 3 kHz), the ELF (3 kHz - 3 Hz) and ULF bands (< 3 Hz ), but sharply decreases for w >> w_o. It is interesting to observe that the limit of S(w)/A(r, q) at low frequencies (w ® 0) increases with decreasing of w_o and shows a maximum for g = w_o. In fig. 1 is represented the frequency dependence of S(w)/A(r, q) for selected values of parameters g and w_o.

Fig. 1 - Dependence of S(w)/A(r, q), Eq. (5), from the angular frequency w (rad s-¹), for w_o = 10⁶ rad s-¹ and g = 2w_o (dashed line); g = w_o (dotted line); g = w_o /2 (continuous line).

Experimental evidence of electromagnetic emissions before the fracture and at the fracture of rocks, crystals and various insulating or quasi conducting materials are well documented in literature. The first report of this phenomenon was given in the 17th century by Otto von Guericke (de Guericke, 1672) who, describing the electrical discharges observed through rubbing on a sulphur globe, says "...it shines in the same way as crushed sugar." Indeed, it is easy to observe, in the dark, the light flashes by crushing transparent crystals like those of sugar. Visible photons during deformation, and prior to failure of MgO single crystals, were detected (Langford, 1987), while electromagnetic emissions from cracked granite were observed (Warwick, 1982). Recently it has been reported the detection of radio noise signals at 500 kHz and at 200 kHz in fracture experiments on gneiss (Mognaschi, 2000). These experiments were performed by applying an uniaxial stress which increased uniformly from zero to rock failure in about 90 s. A magnetic antenna of 107 turns, wound on a ferrite rod, was placed near the gneiss block under uniaxial stress. The antenna, shielded from external noise sources, was connected to a radio receiver tuned at 500 kHz. The audio output was recorded on a tape and then analysed with a dynamic signal analyser Hewlett-Packard 35665A. The time acquisition capability of the spectrum analyser being limited to four seconds, only such time interval is shown in fig. 2. Macroscopic failure of the sample corresponds to the big signal to the right, which lasts about .4 s. Other signals are visible before rock failure. The time dependence of the signals clearly shows their damped behaviour.
 
 

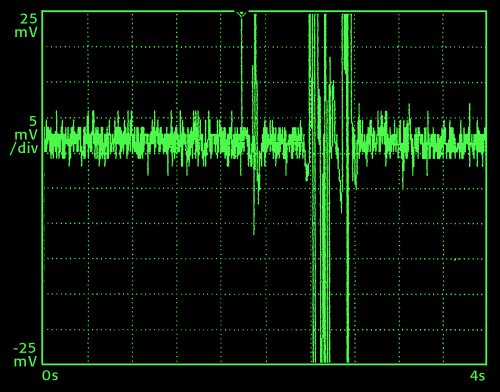Fig. 2 - Part of time dependence of the dynamical analysis of the audio signal, at the output of a radioreceiver tuned to 500 kHz, of electromagnetic emissions produced by a gneiss sample under uniaxial stress. Rock failure corresponds to the big signal to the right; other signals are visible .5 and .6 s before it. On the abscissae axis there is time from 0 to 4 seconds; the ordinates axis refers to the signal intensity with sensibility of 5 mV per division.

Similar signals, in the VLF frequency region, were recorded (Nardi, 2000) before the fracture of various lithotypes for applied stresses slightly greater than a half of those corresponding to rock failure.

In the case of electromagnetic waves, possibly generated in the Earth due to microfracturing processes and which could precede the release of mechanical energy in the form of shock waves, it is necessary to study their underground propagation and their refraction at the Earth/atmosphere boundary.

5. PROPAGATION OF ELECTROMAGNETIC PRECURSORS

On the assumption that electromagnetic waves are generated in the Earth crust due to the stress-induced microfracturing of rocks, through the mechanisms previously invoked, and that the waves are detected at the Earth surface, we must study the underground propagation in a dissipative medium like the Earth crust (medium 1), the refraction and the possible total internal reflection at the Earth/air interface and, finally, the propagation in air (medium 2).

5.1. UNDERGROUND PROPAGATION

The propagation of electromagnetic waves in the Earth crust can be studied taking into account the electrical properties of its constituent materials as well as the frequency of the waves. The Earth crust is, of course, a non-homogeneous medium since different layers or regions have different composition and structure and, therefore, different resistivities and permittivities; however, for sake of simplicity, let us consider, for the moment, the propagation in a medium which is only characterized by the low frequency conductivity s = 1/r , the permittivity e and the magnetic permeability m @ m₀, in other words we do not consider here magnetic materials because most of the rocks are non-magnetic.

The conductivity of the medium leads to a damping of the wave, and affects its velocity v. The complex wave vector k can be written (Stratton, 1941)

k = a + ib         (6)

where

a = (w/v)Ö [Ö 1 + s²/(e²w²) + 1)/2]         (7)

b = (w/v)Ö [Ö 1 + s²/(e²w²) - 1)/2].         (8)

are the phase factor and the attenuation constant respectively.

Two opposite limiting cases are possible, depending on the ratio between conduction and displacement currents. In dielectrics (s/ew << 1) and conductors (s/ew >> 1) eqs. (7) and (8) can assume a simplified form while, in the intermediate case of quasi conductors (0.01 < s/ew < 100) the a and b constants are given, respectively, by the expressions (7) and (8).

Case I: Dielectrics - The displacement current is very much greater than the conduction current i.e. ew >> s . Since, as discussed in the previous section, we are interested mainly in the low frequency part of the electromagnetic spectrum, this condition is fulfilled e.g. in media which are but slightly conducting. In this case

a » wÖ (m₀e)         (9)

and it is possible to define a real refractive index n^I_E which is given by:

n^I_E = a c/w » Öe_r.     (10)

The attenuation constant b is

b » (s /2)Ö (m₀/e ).         (11)

and results independent of frequency, proportional to the conductivity of the medium (Stratton, 1941), and very small because s is very small.

Case II: Conductors - The conduction current is larger than the displacement current, i. e. s >> ew .
This is the common case for most constituents of the Earth crust not only because of their non-negligible conductivity, but also because we are here mainly interested in low frequencies. The real and imaginary parts of the wave vector (Stratton, 1941) are now

a = b » Ö (sm₀ w/2)         (12)

and are both frequency dependent.

The phase factor a determines the velocity of waves through a refractive index n^II_E:

n^II_E = a c/w » Ö (s /2we₀)         (13)

The attenuation constant b is the inverse of the skin depth d which represents the distance at which the field strength of electromagnetic waves is attenuated by a factor 1/e i.e. about 63% or - 8.7 dB. The skin depth being inversely proportional to the square root of frequency, a conducting material acts as a low-pass filter for electromagnetic waves (Kraus, 1953).

Let us consider, at first, propagation through sea water (s » 4 W^-1 m^-1 ). The skin depth d , in this case, is of the order of 1.5 m at 30 kHz and reaches 145 m at 3 Hz. The evaluation of skin depth shows that the detection of possible electromagnetic precursors of earthquakes with origin below the sea is rather unlikely due to the great attenuation of electromagnetic waves in salty waters. On the contrary, the skin depth at 3 Hz of fresh water (s » 10^-3 W^-1 m^-1) is about 9.2 km. This means that even the deepest fresh water lakes do not greatly attenuate ULF waves.

We will now consider the propagation of electromagnetic precursors in the solid Earth crust and we will discuss the conditions under which electromagnetic precursors can reach its surface and then propagate above it. Resitivity of rocks, as reported in the previous section, varies over a very wide range. Let us consider e.g. some representative cases: dry gneiss, or similar rocks, exhibit a resistivity of 3.2 ´ 10⁶ W m (Parkomenko, 1967), the skin depth will range from 16 km at 3 kHz, to 500 km at 3 Hz; for a more conductive rock, like wet granite, the resistivity is 4.4 ´ 10³W m (Parkomenko, 1967) and the skin depth at 3 Hz is about 19 km. For dry soil (r » 2 ´ 10³ W m) the skin depth at 3 Hz is about 13 km, while, for rural ground (r » 3 ´ 10² W m), it decreases to about 5 km.

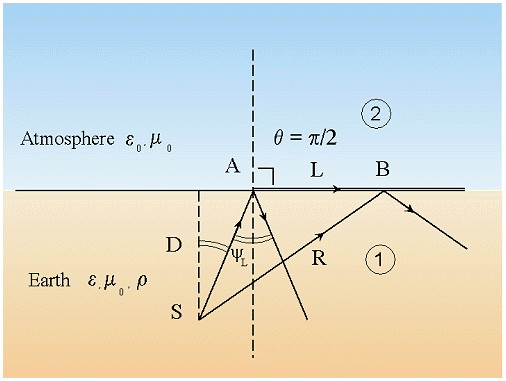
Fig. 3 - Schematic representation (not to scale) of refraction and reflection of electromagnetic waves at the boundary Earth/atmosphere.

This means that the spectral components of electromagnetic signals in the ELF and ULF range, although propagating with attenuation through the Earth crust, could reach the Earth surface with appreciable intensity because the skin depth, in this frequency range and for most constituents of the lithosphere, is comparable or even less than the depth at which electromagnetic precursors of shallow earthquakes have origin (< 60 km).

5.2. REFRACTION AND REFLECTION AT THE EARTH SURFACE

Electromagnetic waves which, from the region of origin, reach the separation surface between solid Earth, supposed flat for simplicity, and atmosphere undergo the phenomenon of refraction and reflection.

If we indicate with y the angle of incidence in the Earth (medium 1) and with q the angle of refraction in the atmosphere (medium 2), see fig. 3, in which e @ e_o and m @ m_o, the Snell refraction law gives

sin y = (1/n_E) sin q         (14)

where n_E is the refractive index of medium 1 previously defined. Eq. (14) implies the existence of a critical incidence angle y_L for which waves will travel in the atmosphere parallel to the Earth surface (q = p /2) as lateral waves (King, 1992). For incidence angles greater than y_L, no refracted wave is admitted. This means that only the waves contained in a cone with semi-aperture y_L could be refracted and then propagate in the atmosphere.

In Case I both the refractive index n_E and the angle y are real. Remembering eq. (10) and that the relative permittivities of dry rocks lie between 4 and 16, the critical angle y^I_L lies between 30° and 14.5°.

In the more common Case II, both the refractive index n_E and the angle y are complex. Physically a complex angle of incidence implies a shift of phase between electric and magnetic vectors and the appearance of an attenuation factor. The Snell law now holds in a formal way with the real part of refractive index given by (13). Notice that, in Case II, the refractive index is a function of the wave frequency. For non-monochromatic waves this introduces an angular dispersion for the outcoming waves. The critical angle y^II_L for which waves would come out from the Earth and travel parallel to the Earth surface (q = p /2) as lateral waves (King, 1992) is given by:

y^II_L @ sin-¹Ö(2we_or),         (15)

For y > y^II_L no refracted waves are admitted. This means again that only waves contained in a cone with semi-aperture y^II_L could be refracted and then propagate in the atmosphere, with negligible losses, at about the speed of light. Fig. 3 gives a schematic representation of refraction and reflection at the boundary Earth/atmosphere. The wave reflected in A is of no interest in the present treatment since it will be absorbed in medium 1, while the total reflection, e.g., in B (y > y_L) gives rise, in the atmosphere, to an evanescent field whose amplitude decreases exponentially with the height above ground and propagates along the Earth surface with an amplitude decreasing with distance as r-² (King, 1992), while attenuation due to losses is practically negligible.

If we now consider e.g. the propagation in a medium of resistivity r = 3.2 ´ 10⁶ Wm, y^II_L values vary from 1.9° at 3 Hz to 19° at 300 Hz, while at higher frequencies the approximation s >> ew is not longer valid. For a medium of resistivity 4.4 ´ 10³ Wm the refractive index at 3 Hz, given by eq. (13), is equal to about 825 and y^II_L is, consequently, very near to zero. The propagation of electromagnetic waves in conductive media, such as those forming the Earth crust, is characterized by very small critical angles and, hence, only rays propagating almost orthogonal with respect to the Earth surface are refracted. The Fresnell’s equations show that, for y @ 0 and q = p /2, the transmission coefficient for the components of the electric field parallel and normal to the plane of incidence is equal to about 2, consequently the electric field intensity of unpolarized waves in proximity of the Earth surface is almost doubled at the boundary Earth/atmosphere. Lateral waves then propagate with negligible losses above and along the Earth surface.

6. FINAL REMARKS AND CONCLUSIONS ON THE DETECTABILITY OF ELECTROMAGNETIC PRECURSORS

Under suitable conditions the low frequency electromagnetic waves, generated in the rocks of the Earth crust under tectonic stresses of the order of about a half of those needed for rock failure (and consequent generation of seismic shocks) can propagate in the lithosphere and reach, as seen previously, wide regions over the Earth surface. However, two distinct paths are possible: i) a path SAB which is partially underground and partially in the atmosphere as a lateral wave; ii) a direct underground path SB, see fig. 3. In path i) there is attenuation due to the conductivity of the medium in the underground part, which practically coincides with the depth D of the source since y_L is usually small, while practically no such attenuation occurs in the atmospheric part of the path; as for path ii), which is of length R, the same attenuation factor is present as in the first part of path i) provided that the medium is homogeneous and isotropic.

The power spectral density of electromagnetic waves produced by damped oscillations is practically independent on frequency at low frequencies, see eq. (5), while the wave attenuation in the underground path is lower for the lower frequencies, see eq. (12). On the other hand, natural electromagnetic noise of galactic origin increases with the inverse of frequency. From these considerations one can deduce that it should exist a frequency range, a "window" (Dea et al., 1993), for which a compromise between wave attenuation and increase of natural noise would give the best chance in the detection of electromagnetic precursors. Such a frequency range would, of course, depend also on the electrical properties of the rocks in the underground path.

Earthquake electromagnetic precursors events were defined by Dea et al. (Dea et al., 1993) as "events with elevated broad-band signals in the 0.1-20 Hz region appearing several hours to several days in advance of moderate to large earthquakes". The same authors have published recordings and data on the increase of power spectra noise in the 1-5 Hz range that were taken one or two days before many moderate magnitude earthquakes in California.

If we consider again the propagation in wet granite from (12) we have at 3 Hz, b = 5.2 ´ 10-⁵ Np m-¹. Assuming for the source depth D the maximum value of 60 km and AB = 80 km the attenuation due to the conductivity of medium 1, would be - 27 dB for path i), and - 45 dB for path ii), respectively. To such attenuation one must add the geometrical field attenuation due to propagation of, e.g., spherical waves. If we admit a radius of one kilometre for the source of spherical waves and we consider a path SB of about 100 km the 1/r factor for the decrease of field intensity will contribute an attenuation of - 40 dB so that the overall attenuation for path ii) will be - 85 dB. As concerns path i), the total attenuation is the sum of that in SA due to conductivity, which amounts to - 27 dB, plus the one due to geometrical field attenuation of spherical waves, which amounts to - 36 dB, plus that of lateral waves in AB, which amounts to - 14 dB. The overall attenuation along path i) being - 77 dB, which is lower than that along path ii) previously calculated. The attenuation along path ii) is, therefore, the one which impose constraints to the detectability of electromagnetic waves.

The field intensity at the receiving station must be, of course, greater than the natural radio noise. Assuming an average level for the natural noise, in the frequency interval from 1 to 3 Hz, of 1 mVm-¹, an attenuation of - 85 dB requires that the power of an hypothetical isotropic radiator at the source, supposed in free space, should be of about 50 kW in order to produce an electromagnetic field greater than 1 mVm-¹ at the receiving station. This estimated power is rather small compared with the huge powers involved in microfracturing of geological structures of the Earth crust, so that it is not unlikely the existence of mechanisms, as discussed in section 4, which could generate electromagnetic waves with the required strength.

On the other hand, lateral waves travel in air at about the light speed c, while underground propagation takes place at speed v = c/n_E which could be much lower than c. The time delay between signals which travelled along the two paths, in the case considered, is mainly determined by the difference of length between the two underground paths SA @ D = 60 km and SB @ 100 km, and amounts to 100 ms, a time delay easily measurable.

It could be possible, by means of a network of stations, to localise impending earthquakes through the time delay of arrival of the two types of waves, provided the speed of the underground electromagnetic waves is known at least to the same relative accuracy with which the speeds of elastic waves in the lithosphere are known.

As for the detection of electromagnetic precursors by means of a couple of electrodes driven in the soil at a distance of some tens or hundred of meters between them, the sum of electromotive forces due to the horizontal components of the electric field of the waves which have travelled along paths i) and ii) will be picked up and an analysis of the time autocorrelation of the received signal is to be performed.

At larger distances from the source S the attenuation of underground waves will prevent their detection, while the lateral wave could be still received.

The treatment and the considerations developed in the present paper were brought about with the aim of finding a theoretical support to the explanation of the origin, propagation and detectability of such electromagnetic precursors and eventually to propose a method to localise their origin which could coincide with the focus of a forthcoming earthquake. In presence of some experimental confirmations of the simple model we propose, it would be worthwhile to afford a more realistic description of the Earth structure and properties by taking into account other important details as, for instance, the layered structure of the involved media.

At present very effective methods of seismic exploration are based on the recording and analysis of acoustic lateral waves. The application of the same techniques to electromagnetic precursors of earthquakes could be effective to predict where tectonic stresses have increased to above a half of the failure value of rocks and hence to localise the focus of a future earthquake; from the evaluation of the strength and a study of the time evolution of such precursors, it could also be possible to estimate in advance the earthquake magnitude and when the rocks failure, which will originate an earthquake, will take place. To reach such goals the dynamics of rocks fracture processes should be fully understood and the data on electromagnetic precursors should be carefully collected and analysed.

At present an experimental activity is under way in order to analyse experimental data on the natural radio noise in the ELF and ULF bands along the lines above outlined.

Note added in proof - After the submission of this paper an experimental confirmation of the previsions based on the above theoretical model was found in a recent paper (Varotsos et al., 2001). A delay up to 1-2 s in the time of arrival at the Ioannina station (at an epicentral distance of about 80 km) among two kinds of electromagnetic signals was detected 3 weeks before the 6.6 Grevena-Kozani earthquake occurred on May 13, 1995. The first signal arrived was detected as low frequency electric field variations, while the delayed signals were detected as low frequency variations of magnetic field intensity obtained at a sampling rate of 1 sample/sec. This time delay cannot be attributed neither to the instrumentation, nor can be present in signals due to nearby artificial sources. It could be explained as due to different velocities of propagation of electromagnetic waves along different paths.

ACKNOWLEDGEMENTS

Very useful discussions on the propagation of electromagnetic waves in dissipative media with prof. G. Campagnoli and his critical reading of the manuscript are gratefully acknowledged. Thanks are also due to the referees prof. R. Cassinis, dr. A. Marcellini and prof. G. Siragusa for suggestions and observations which were taken into account to improve the paper.

REFERENCES

Båth M. (1973) - Introduction to Seismology. Birkhäuser Verlag, Basel, 395 pp.

Bieniawski Z. T. (1967) - Int. J. Rock Mech. Min. Sci., 4, 407-23.

Chakrabarti B. K. & Benguigui L. G.(1997) - Statistical physics of fracture and breakdown in disordered systems. Clarendon Press, Oxford, 161 pp.

Dea J. Y., Hansen P. M. & Boerner W-M. (1993) - Long-term ELF background noise measurements, the existence of window regions, and applications to earthquake precursor emission studies. Phys. Earth Planet. Interior, 77, 109-125.

Gross S. P., Fineberg J., Marder M., McCormick W. D. & Swinney H. L. (1993) - Acoustic emissionsfrom rapidly moving cracks. Phys. Rev. Lett., 19, 3162-3165.

de Guericke O. (1672) - Experimenta nova (ut vocantur) magdeburgica de vacuo spatio. J. Janson, Waesberg, in latin, 244 pp; see also von Guericke O. (1994) - The new (so-called) Magdeburg experiments of Otto von Guericke on empty space. Kluwer Academic Press, Dordrecht, 394 pp.

Gutenberg B. & Richter C. F. (1954) - Seismicity of the Earth. Princeton University Press, Princeton, 310 pp.

King R. W. P., Owens M. & Wu T. T. (1992) - Lateral electromagnetic waves: theory and applications to communications, geophysical exploration, and remote sensing. Springer, New York, 740 pp.

Klyuev V. A., Lipson A. G., Toporov Yu. P., Aliev A. D., Chlyk A. E. & Deriaghin B. V. (1984) - Charactericescoye islucenye pri rasruscenii tverdikh tel i naruscenii adgesionni sviasei b vacuume. Dokl. Acad. Nauk SSSR, 279, 415-19, in russian.

Kraus J. D. (1953) - Electromagnetics. McGraw-Hill, New York, 604 pp.

Langford S. C., Dickinson J. T. & Jensen L. C. (1987) - Simultaneous measurements of the electron and proton emission accompanying fracture of single-crystal MgO. J. Appl. Phys., 62, 1437-1449.

Matsuda T., Yamanaka C. & Ikeya M. (2001) - Behavior of stress-induced charges in cement containing quartz crystals. Phys. Stat. Sol. A, 2, 359-365.

Meloni A., Di Mauro D., Mele G., Palangio P., Ernst T. & Teysseire R. (2001) - Evolution of magnetotelluric, total magnetic field, and VLF field parameters in Central Italy. Ann. Geofis., 44, 383-394.

Mogi K. (1973) - Rock Fracture. In: F. A. Donath, F. G. Stehli & G. W. Wetherill (eds.) - "Annual Review of Earth and Planetary Sciences", vol. 1. Annual Rev. Inc., Palo Alto, 350 pp and references therein.

Mognaschi E. R. & Zezza U. (2000) - Detection of electromagnetic emissions from fracture of rocks and building stones under stress, paper psented at 5th International Congress on Restoration of Architectural Heritage. Florence, p. 553 - 562.

Nardi A. (2000) - Evidenze di emissioni elettromagnetiche in rocce sottoposte a sollecitazione meccanica. Un possibile prcursore sismico?, Thesis, University of Rome, Rome, in italian, 193 pp.

Parkhomenko E. I. (1967) - Electrical Properties of Rocks. Plenum Press, New York, 314 pp.

Reynolds H. R. (1961) - Rock Mechanics. Crosby Lockwood & Sons, London, 136 pp.

Scholz C. H. (1968) - Microfracturing and the inelastic deformation of rock in compression. J. Geophys. Res. 73, 1417-32.

Stratonovic R. L. (1967) - Topics in the Theory of Random Noise, vol II. Gordon and Breach, New York, 329 pp.

Stratton J. A. (1941) - Electromagnetic Theory. McGraw-Hill, New York, 615 pp.

Teisseyre R. & Ernst T. (2002) - Electromagnetic radiation related to dislocation dynamics in a seismic preparation zone. Ann. Geophys., 45, 393-399.

Varotsos P., Sarlis N. & Skordas E. (2001) - Magnetic field variations associated with the SES before the 6.6 Grevena-Kozani earthquake. Proc. Jpn. Acad., B - Phys. and Biol. Sci., 77, 93-97.

Warwick J. W., Stoker C. & Meyer T. R. (1982) - Radio emission associated with rock fracture: possible application to the great chilean earthquake of May 22, 1960 . J. Geophys. Res., 87, 2851-2859.

Final version received 6th November, 2002

Return to the main index