Multi turn wire loops are often used as low frequency receiving antennas. Applications such as geophysical research, oil exploration and survivable communications require maximum sensitivity of receiving loop antennas. The loop sensitivity decreases as frequency decreases, becoming a formidable problem below 1 Hz. Basic electromagnetic theory is developed here as it relates to electrically small multi-turn loops at low frequencies. Simple algebraic expressions are produced describing the sensitivity of loops in simple geometries. The concept of antenna factor (effective aperture) is introduced, which allows comparison of different loops, and conversion of observations to common magnetic units of measure. It is hoped this work will be a useful reference to geophysical researchers, and to anyone designing loops for low frequencies.

INTRODUCTION
Magnetism is manifested as a 'field of vectors', that is, any point in the magnetic field has not only a magnitude, but a direction in space. The four Maxwell equations describe how electric and magnetic vector fields behave and interact. These "fields" are actually primordial root forces and motions of our spacetime continuum. It is well said that all the laws of physics can be derived from the Maxwell equations, given here in integral form:

According to Maxwell, an electric field cannot change without creating a magnetic field, and a magnetic field cannot change without creating an electric field. Any change in one force field creates a vortex or wake in spacetime appearing as the other aspect of the force. Electromagnetic waves have both electric (E) and magnetic (H) components, and propagate as ripples in the fabric of our continuum. The E and H aspects appear 90 degrees apart in space dimensions and in phase in the time dimension. Loops of wire are often used as antennas to interact with and detect the magnetic aspect of the electromagnetic force.

Suppose we have a varying magnetic field 'out there' which we want to detect and measure. This field may originate naturally or artificially. To make the analysis more tractable, the loop is assumed to be electrically small, the dimensions being much smaller than a wavelength of the frequencies of interest. We also take the distance to the source as being much larger than the loop dimensions. These conditions are usually well satisfied in geophysics. We will use vector calculus to derive from first principles the response of such a loop. Those unfamiliar with this branch of mathematics may skip down to equation (10), where the going gets easier.

THEORY OF MAGNETIC LOOPS
Magnetic field intensity, H, expressed in units of amperes per meter, produces a magnetic flux density , B, expressed in volt seconds per square meter. Flux is proportional to applied field.

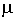, expressed in Henrys per meter, is the magnetic permeability of the medium, the analog of electric permitivity. We will let 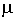 equal 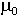, the permeability of a vacuum (spacetime itself). This assumption is well justified for air core loops surrounded by non magnetic media, including air, water, dirt, vegetation, etc.

The total magnetic flux, , in volt-seconds, threading an area is the flux density integrated over the area. The vector n denotes a unit vector normal to da, the element of the surface being integrated over.

Voltage around a loop is proportional to the rate of change of the amount of flux threading the loop area. When multiple turns are in series, the total voltage is the sum of the individual turns.

Notice from (3) that a motionless loop in a constant dc field produces no voltage. Combining these three equations gives an expression for the terminal voltage of a multiturn wire loop. The vector normal component of the H field is integrated over the loop area, and differentiated by time.

When the H field is uniform over a planar loop, we can take H out of the integral and express its vector normal component as the magnitude times the cosine of the angle between the H vector and the loop axis.

and the integral becomes simply the loop area.

Most of the calculus is solved, but the time derivative of H remains. We can reduce it to simple algebra by examining a discrete frequency (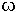t) component of H, with peak amplitude Ho.

Which transforms equation (6) into:

So we now rid ourselves entirely of calculus:

Taking the magnitude of the signal, we get loop terminal voltage as a straight algebraic product of six terms;

The persistent product of N and A are the only remaining terms which describe characteristics of the loop itself. This product suggests a figure of merit for loop antennas, the "effective aperture", Ae , which is the physical area times the number of turns.

We can now express the on-axis sensitivity of a loop, which is the terminal voltage divided by the applied magnetic field, as the product of only three terms:

Equation (11) clearly shows the problem of loops at low frequencies: as f approaches zero, so does the loop voltage! Although we can't do much to change 2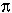, we might try increasing 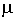 above 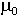 by using a ferrite loop core, but this becomes impractical with large areas. Our only recourse is to increase the effective aperture.

EFFECTIVE APERTURE
We now have a rigorously derived expression for loop antenna sensitivity, reduced to the simple product of three terms, a constant, the frequency, and the effective aperture, which is the antenna factor. By knowing the effective aperture, we can relate the loop output back to the magnetic field strength. We can also compare the sensitivities of different loops, making possible the correlation of data from researchers using different loops. This effective aperture is simply the loop area times the number of turns, expressed in square meters.

The areas of some common loop geometries are:

MAXIMIZING AE
For maximum sensitivity, we want maximum effective aperture. Practical limitations dictate the effective aperture we can achieve. For example, we might be limited to 5lb loop mass of copper wire, and can handle wire as small as #30 AWG. What is the maximum effective aperture we can achieve?

From the NIST copper wire tables we get: wire diameter = 0.010 in, length = 16435 ft, and resistance = 526 ohms. For a circular loop, the wire length and loop area are:

So the antenna sensitivity for a fixed wire length is :

The d term appearing in the numerator tells us to deploy a fixed length of wire as a single turn for maximum sensitivity. The diameter will then be :

With an antenna factor of:

A large effective aperture, but our trepidation in handling a one mile diameter loop of #30 AWG wire leads us to now limit the loop diameter to ten feet. Equations (12) through (14) give us:

This is a manageable structure, but sensitivity has been reduced 523 times.

Some rules of thumb for loop sensitivity are:

• For a fixed number of turns:

Sensitivity goes up as loop diameter squared, and up as wire length squared.
• For a fixed wire length:

Sensitivity goes up as the loop diameter, and down inversely as the number of turns.
• For a fixed loop diameter:

Sensitivity goes up as number of turns, and up as wire length.

PRACTICAL EXAMPLES AND CONSIDERATIONS, THE OCTOLOOP
Of several shielded loops I recently made, one in particular, the "octoloop" stands out in performance and ease of construction.
The 'octoloop' is an easily built, well shielded, VLF loop, small enough to gimbal, which was my primary design goal.  The octoloop characteristics are:

        A  = 3.42        m^2 

        N  = 50         turns 

        Ae = 171         m^2

        A  = 1865        m^2
        N  = 12         turns
        Ae = 22,381      m^2

The octoloop in the following example is a length of 25 pair telephone wire inside an octagonal loop shield of 3/4 hard copper pipe. Mine is about 7 ft dia and wired for 50 turns, and gimballed for noise rejection. The pipe shield is a very effective electrostatic shield at MF, and also reduces VLF/ULF microphonics, which for obvious reasons plague most loops. The self resonant freq has not yet been measured, but is probably near 12 kHz.

I took the octoloop to the backyard and leaned it against a tree, oriented to null the noise. For the first time ever, I was able to tune my Rycom 6040 to 0 Hz and hear something besides BUZZZ! The loop has good sensitivity with an almost perfect noise null, a real pleasure to operate! I clearly heard FIVE of the eight OMEGA stations, a NiCd battery charger 450 ft away, and some tweeks and pops. Even inside the house, I hear OMEGA, WWVB and the stronger sferics.

The octoloop is easy to make for about $20. You need some 3/4 in hard copper pipe, eight 45 deg elbows, and two male threaded adapters. You also need a 3/4 inch sealed conduit body tee, a 3/4 CPVC coupling, enough 25 pair cable to go around the loop, and your favorite connector.

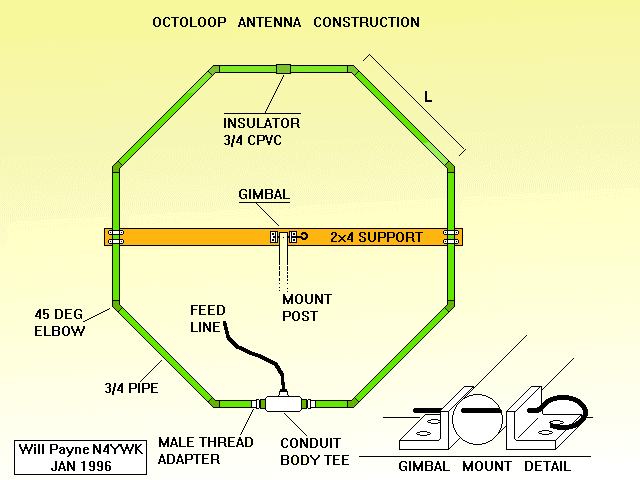
Cut eight pieces of pipe to length "L" to make your loop the desired size. The finished diameter will be 2.41*L and the circumference will be 8*L. I used 36" for L, giving a finished size which barely passes thru my basement door. Now cut two pieces in half. Sweat two of the L/2 pieces into the male adapters, thread them tightly into the conduit body, and trim off both ends to reduce the total length back down to L.

At this point you should have eight pieces of length L, with one cut in half, and one with the conduit body inserted into it. Sweat the ends of the pieces and the elbows with solder. Lay out the octagon on a flat surface with the L/2 pieces opposite the conduit tee. Sweat together. Allow to cool, then clean.

Now to pull the cable through. Tie a thread to a small cloth rat and blow it through one half of the loop using a shop vac or hair dryer. Next, pull a strong cord through. Use wire pulling lube or liquid soap to help pull the wire through one half of the loop, starting in the conduit body. Doing each half separately makes a hard pull easier. Clamp the work in a vise or conscript a friend or family member if necessary.

IMPORTANT NOTE: slip the 3/4 inch CPVC coupling over the wire before pulling into the second half! Continue in the same manner to complete the loop. When the wire pulls tight, it should pull the two L/2 pieces snugly into the CPVC coupling. This insulator is important to prevent the shield from becoming a shorted turn.

If you used 25 pair cable, you have 50 turns to splice together. I used solder and shrink tubing to splice together ten 5 turn windings which can be put in parallel for 5 turns or in series for 50 turns. Splicing took me less than two hours. Mount your favorite balanced connector in the third port of the conduit tee, or use a bushing to pass a balanced cable. I use XLR microphone connectors and mic cable for balanced loops. A small preamp may be put inside the conduit body. My octoloop is mounted via cable clamps on a 2x4 with a gimbal in the center.

This construction technique is my favorite so far. It is easily extended to 24 ft dia, and further with modifications. There are also several ways to get more turns. I hope those who make octoloops will report their results and the improvements which they will undoubtedly make!

Obviously, the fixed loop is more sensitive, by a factor of about 130. In antenna terms, this is a gain increase of about 42 db, a substantial improvement! However, if by gimballing the octoloop, I can get a 50 db deep null in interference, and stay above my receiver noise floor, the octoloop still has an 8 db advantage. On the other hand, with the fixed loop, if I filter out the power grid interference, I can go 130 times lower in frequency before falling below the thermal noise floor.

The octoloop is more useful for sferics and OMEGA reception, but the fixed loop is capable of deep infrasonic frequencies and geomagnetic work. Below some point in the spectrum, one must forego gimballing and portability to gain very large antenna effective apertures. Larry Grant's "Life at 1200 Turns" loop probably has an aperture near Ae = 2000 m^2, approaching the practical limit for portable loops. In oil exploration, loops of several hundred feet of multiconductor cable are transported by rolling them up on spools.

OTHER FACTORS
If an electric current flows in the loop, the terminal voltage and the sensitivity will be modified from that derived above. Current may be drawn by resistively loading the loop output, which will decrease the available voltage. Parasitic capacitance, as well as external capacitance will also cause a current flow, but one which is leading in phase. Capacitance neutralizes the lagging phase of the loop inductance and causes a frequency resonance, increasing the aperture while reducing the bandwidth. The magnitude of these tuning effects are maximum when loop resistance is minimum. Capacitively tuned loops are useful for their sensitivity to a single discrete frequency.

Mechanical motion of a conductor in a steady DC field induces a voltage, leading to microphonic effects. Microphonics may be reduced by structural stiffening and damping, to reduce vibrational resonances and shift them out of the frequency bands of interest. Many loop structures will have an axis of minimum vibrational response, which may be aligned with the local field to further reduce microphonics.

Temperature effects in dissimilar metallic junctions cause Seebeck voltages to be produced, which generally have time constants as long or longer than the thermal cycle. Temperature also causes voltage drift in high gain DC coupled amplifiers. Thermal effects may be controlled by isolating amplifiers and metallic junctions from temperature changes, by DC blocking, or by chopper stabilizing DC amplifiers.

DIRECTION OF FUTURE WORK
The fixed loop was originally intended for OMEGA (the 10 to 14 kHz squeal) reception, but Larry Grant and Bob Confrey have me interested in geomagnetics. Presently, I am working out an improved preamplifier design for geomagnetic frequencies. I am convinced the best way to go is a fixed moderate gain first stage at the loop, using a biomedical instrumentation amplifier such as Analog Devices AD620, and then put more gain with adjustments, filtering, etc in a separate indoor unit. For large aperture loops, the preamp must tolerate very high 60 Hz hum levels without desensing or intermodulation.

Also I am looking for yet more antenna aperture. Just today, I screeched my truck to a halt and leaped into a muddy excavation wearing my good pants because I believed I saw an abandoned length of 600 pair telephone trunk cable. The area of my backyard is about 6300 m^2, which enclosed with 1200 turns (600 pair) would give Ae = 7,500,000 m^2. This would be the most sensitive loop I know how to make here, having three times the aperture of the hypothetical one mile turn of wire discussed above, and should be useful to below 0.01 Hz.

A DC block below 0.001 Hz or so will be required to remove the Seebeck potentials from 1200 spliced joints, and the antenna may be buried to reduce microphonics. I am at a loss for a feasible method of removing seismic microphonics, which I believe will appear as the next envelope boundary, although seismic microphonics may in themselves be a worthwhile study.

Acknowledgements
I would like to thank Bob Confrey for sparking my interest in geomagnetics, Larry Grant for his landmark practical design, and Anthony Fraser-Smith for his pioneering work. I also want to thank Dr. John Weaver, Dr. Walter Nunn, and L.A. (Kip) Turner for mentoring and inspiring me throughout the years.

This article is protected under US and international copyright laws. Please obtain the author's permission before redistributing this document or reproducing it in any other form.

Return to the main index