1. Preface
2. Introduction
3. Direction
finding in general
4. EM
field reception at VLF
5. Direction
finding at VLF
6. Representation
of multiple dimensions
7. Processing
on a computer
The following ideas are presented to the private
research community, hoping to inspire their work, without commercial interest.
This is meant as an initial part of the development of an advanced and
versatile signal tracking and analysis tool. Possible applications are
not limited to a single field of interest. Most of the content is a summary
and combination of ideas that were already made by others. I want to encourage
those, who have the required programming skills, to continue this. If referring
to this text, I only want that to be mentioned.
Introduction
As the techniques for reception of electromagnetic signals become refined, the more signals show up that were not seen before. This leads to a situation where the diversity of information available from the signals becomes hard to separate. Based on this I made some thoughts about the possibilities for analysing and representing them.
The distinguishing dimensions of information available from the waves are:
In the case of far fields it expresses itself in travelling time, intensity and as dispersion within some media of propagation. Travelling time can be determined if the time of transmission is known. The difference in time of arrival at different loctions can be used to determine the location of the source whithout knowing the time of transmission. This is used with ground based networks for lightning detection and localization. Intensity is also depending on parameters as radiation power and propagation losses, which are often unknown. Determining the time of travel or length of the propagation path from dispersion presupposes knowledge of the dispersive properties in the medium. Dispersion transforms short EM events into long whistlers for example.
With near fields distance from the source is also found in the intensity gradient. In order to detect this, there are two reception systems necessary for each type of wave and direction. For detection of distance with sources from all direction in the plane of the earth's surface there must be at least three omnidirectional antennas.
As reception is often from a far field and to keep
things not too complicated, I will discard detection of distance. The location
of a source can mostly also be estimated by direction findings from at
least two distant receiving lacations.
Direction finding in general
There is a long history in determining the direction of radiation of any kind, as it is a fundamental task for navigation and object localization for most living beeings. EM waves have been used for this even before knowing of their electromagnetc nature for example with detection of warm objetcs by animals and the whole human astronomy is based on it.
Finding the direction and locations of transmitters of manmade EM waves is common practise with navigation in the air and on the water mainly using beacons in the LW and MW range. Radar is another kind of radio direction finding (RDF) using much higher frequencies.
Tracing a transmitter and determining its location, for example with radio amateur's fox hunting, is closely related to RDF. This mostly involves more than one location of reception in the case of great distances as the field gradient is neglectible in this case. Large networks have been built for tracing events and objects within wide areas for civil and military tasks. Examples of such and related networks operate for lightning detection, radar monitoring, investigations in astronomy, space physics and earthquakes.
Determining the location of a receiver using well
known transmitter locations is a similar task, usual for navigation purposes
with radio beacons. Direction finding does not necessarily need to be involved
in receiver localization when using information from the wave in the time
domain only. Examples are
EM field reception at VLF
In VLF there are not all types of waves equally present. In the vicinity of the earth's surface the waves due to far field sources consist mainly of a vertical electrical component and the corresponding magnetic waves with horizontal polarisation. In order to get all the information available in these waves we may use one electric vertical antenna and two magnetic horizontal antennas which are arranged right-angled to each other. In order to get true far field information not distorted by effects of local installation, these antennas should be influenced by their surroundings as little as possible. This means absence of magnetic guides like large objects of steel in the vicinity or electrical field deformers like trees, buildings or fences.
In order to obtain the information that is contained in these signals, there must be three independent receivers/amplifiers which must produce virtually no difference in phase shift throughout the frequency range of interest.
It's a premise for the following to work that the
signals to be multiplicated are not distinct in phase by 90°. The far
field of an EM wave inherits the required property and the antenna systems
must not change that. As an inductive antenna for magnetic field induces
a voltage that is phase-shifted by 90°, this has to be corrected by
an integrator or by an amplifier as described by Marco Bruno with his article
"THINKING ABOUT IDEAL LOOPS".
Direction finding at VLF
The detection of direction is not so common in VLF reception, so I want to describe that now. It is practiced by several investigators to turn a magnetic reception antenna in space, in order to minimize the intensity of interfering signals from fixed sources of radiation. With a well shielded or symmetrical magnetic antenna there usually are two opposite directions of minimal reception for each source. Turning the antenna away from this causes signals with opposite phase depending on the direction of misalignment and an amplitude that is proportional to the cosine of the angle. Therefore the combination of two orthogonal magnetic reception antennas allows determining the direction of an arriving wave when comparing their signal strength and phase with regard to each other. There only remains an uncertainty of 180°, as waves originating from exactly opposite directions give the same result, although the absolute phase is different in each case. To overcame this, the received signal from the electrical vertical antenna must be taken into account as a reference, which is independent of the source direction regarding phase and amplitude.
Let's consider this in the case of one single frequency. At first we perform a multiplication of one of the B-field signals with the E-field signal. The E-field signal is independent from the source direction. Amplitude and phase of the B-field signal are determined by the cosine of the angle between the coil axis and the direction of the incoming wave. What we get is a sum of two mixing products, one of doubled frequency (which is uninteresting) and a DC component, which is proportional to the cosine of the misalignment angle of the magnetic antenna. This DC can be positive or negative depending on the direction of the source relative to the orientation of the coil. Presupposing that we receive a wave of constant amplitude we can then make a plot with the angle between antenna axis and wave direction for the x axis and the amount of the DC for the y axis. The result is a cosine curve with one periode for 360°. Now we take the signal from the second magnetic antenna, perform the multiplcation with the E-field signal and add the second plot to the same diagram. Now we have two cosine curves with a phase shift that is equal to the angle made by the antennas. If the second antenna is rotated by 90° compared to the first, their output signals are independent and the corresponding DC values are appropriate to be used as x and y coordinates describing the direction of the incoming wave.
The necessary multiplications can be automatically
performed in real time for example using two analog mixers. Removal of
the doubled frequency components requires low pass filters only.
Representation of multiple dimensions
This information of direction can be presented directly in a graphical way using a display that shows some kind of pointer from the a central point representing the receiver location to the direction of the source. As the amplitude of the incoming wave is determined by several unknown factors it will be sufficient to reduce the direction information to a point on the circumfence of a circle with a constant radius. Now we can combine these two dimensions with those of frequency, intensity and time.
The next item shall be frequency. The use of spectrograms is widespread and very useful in analysing VLF signals. They can be generated in real time not only using separate spectrum analysers but also by means of software on the PC using fast Fourier analysis (FFT). When such an algorithm of analysis is combined with the one for direction finding and display, we can let the output of the FFT show up in the direction display. It seems reasonable to me, when the dimension of frequency is represented as the distance from the central point in the display, resulting in concentric circles for each frequency. Thus direction and frequency are combined to be represented as two-dimensional information on the display. There must be FFT for all three channels and evaluation of direction must be performed for each frequency separately. The complexity of the necessary calculations is much expanded now and utilization of a digital signal processing (DSP) system will be inescapable. A fast processor of a PC may be appropriate.
Intensity can be introduced to the display simply as intensity of light on a black background. This will be more informative and better readable when using a colour scale. In order to cover a larger scale of intensity, the scale can be logarithmic.
The information on intensity can be derived from the root of the sum of squares of the two DC values. The resulting value describes the power density of the far field, thus weakening the influence of near field sources. This is a useful feature, as the fields from near sources have strong electric or magnetic components but not always the combination of both. If those are of special interest, the source of intensity information may also be chosen to be an according combination of the two B-channels or the E-channel only.
If the whole thing is made to operate in real time, changes in direction or frequency will show up as movements on the display and changes in intensity will show up as variations of lightness or colour.
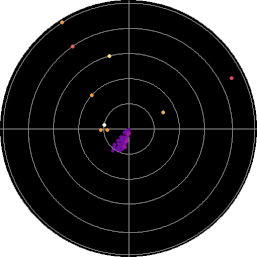
The display may look like this example:

The frequency range is imagined to be set to 0...256Hz. On the left we can see 50 Hz power grid hum with harmonics arriving from slightly different directions, on the rigth there is a field from a PC monitor with a vertival frequency of 75Hz. At 150Hz both harmonics add to any coincidental direction. At 45Hz and 55Hz we can see an additional source which may be a motor driven machine producing sidebands to the center frequency given from the power line. Below 50Hz there are some weak Schumann resonances arriving from random directions, mainly from the south. In this example local sources of radiation are predominant with much inaccuracy of direction reading. This will be much more precise with signals from far field sources at higer frequencies. Nevertheless the Schuman resonances are well separated by direction. Tweaks will show up as flashing lines in radial direction and whistlers will be seen as spots that quickly move towards the center. VLF signals produced from transmitters like the alpha and omega system will show up as blinking dots at fixed locations within the display, while noise will pruduce a random background.
A very crudely approximated measure of distance
can be obtaind from the reciprocal value of the measure for intensity,
preferably with a logarithmic scale for coverage of a wide range. Thus
calculated "distance" may be displayed as distance from the central point
of the display and a coarse frequency information can be added as the colour
of the point.
Processing on a computer
If these operations are performed on a computer, it is also possible to generate the display as additional processing on a three-channel audio input from files. Generated this way or in real time, the results can always be stored as a file, which allows for later examination, unlimited distribution and repeated view, even in slow motion or reversed.
As all these operations are performed, it is also possible to show the results with another view. Time can be chosen for the x axis and any arbitrary dimension for the y axis, for example over-all intensity or that of one certain frequency, over-all direction or that of one frequency, omnidirectional frequency plot or on one special direction.
As hardware for the reception system, besides the three input amplifiers, a sound input device will be needed that supports three channels. This is not a problem, as the use of more than one soundcard is supported with several computer operation systems.
In principle the amount of data increases with the examined bandwith, while the product of the maximal number of frequency bands and intervals per second is constant. Discarding available frequency bands from FFT is essential when the sampling rate of the sound input device is higher than necessary for the frequency range of interest.
In order to get a reasonable amount of output data with increasing frequency range the precision of information may be reduced. Reduction in the time domain is done by averaging of consecutive chunks of data. Noise will show up as points jumping and wriggling around. This can be reduced by avearging in the time domain, simultaneously loosing precision of direction and intensity for short events. Precision with time can be maintained by choosing shorter time intervals and averaging of consecutive data chunks again. Thus the number of frequency bands is reduced. This can also be done after FFT by averaging of the information from adjacent frequency bands.
A useful file format has to be defined for recording
the results of the analysis.
In order to maintain completeness and flexibility
with an amount of data as
small as possible I suggest this file format should
contain
Redundant information is introduced in order to allow streaming and display or storage of partial content of a continuous stream even when its beginning is not available.
A program serving all these tasks may allow to
Peter Schmalkoke, May 2001