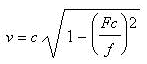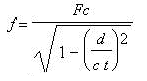SIMPLE
EARTH-IONOSPHERE WAVEGUIDE CALCULATION
By Alves Thierry,
24 august 2003, Cicouro, Portugal.
This paper tells about
the propagation of a wave in the earth-ionosphere waveguide, about spherics,
and their well known dispersion giving the birth to the well known tweeks.
I write this paper thanks
to my observations of the VLF sounds, you will find here some thought about
VLF propagation. Please don't take all of it as true things, the bigger
part are suppositions, so I want your opinion about that.
THE EARTH-IONOSPHERE
WAVEGUIDE
We are going to imagine a rectangular waveguide,
because a spherical one, is to much complicated to study. The " walls "
of the waveguide are composed by the earth ground and the first stages
of the ionosphere, the D layer in day time and E layer in night time.
THE GROUND WALL
The ground is a conductor thanks to the very little
mineral particles that it contains, the salt for example is used to increased
the ground conductivity near the electrical grounded installations. The
water is also a conductor, but it's a better one. Pure water is a no conducting
material, because it doesn't contains mineral particles.
In this paper, we will assume a perfect reflecting
ground with infinite conductivity, with no absorption of the waves.
THE IONOSPHERIC
WALL
Because of the solar ionization and also other
smaller ionization effects as meteors, or even high energetic radiation
from the space infinity, the ionosphere becomes a conducting wall that
can reflect the waves, as light is reflected on a mirror.
In this paper, we will assume a perfect reflecting
ionosphere, with infinite conductivity, of course it's not true, but in
this way the calculations are really simple.
THE LIGHTNING
We will also imagine a storm in this waveguide.
The lightning is composed by two parts: first a thin channel growing from
ground to cloud called in french " Feux de Saint Elme ". Secondly a bigger
channel called " return stroke " goes from the cloud to the ground thanks
to the first thin channel, and because of his high speed, a quarter of
the light speed, we hear the well known noise: BROOUUMM!!!
The return stroke radiates the bigger part of the
signals we are able to listen in our receivers, this ones are called spherics,
tweeks, or whistlers, it depends in the propagation path of the signals
coming from the return strokes, for the two first signals, it's the waveguide
mode propagation, for the third signal it's the magneto-ionic mode propagation.
In this paper we will only speak about the waveguide mode.
THE WAVEGUIDE
PROPAGATION
(ALL OF THIS CHAPTER IS WRITE WITH MY SUPPOSITIONS,
I'M NOT SURE THAT ALL OF IT IS TRUE)
A return stroke is able to radiates in all the electromagnetic
spectrum, and so in the radio spectrum, from SLF to SHF. Spheric noise
are well heard in summer time on short wave frequencies. A return stroke
radiates the bigger part of energy around 6-7 Khz. Sometimes on HF or VLF
band some big spherics are heard, it's the signification of a coming storm.
By learning to recognize this strong spherics, we can easily predict the
arrival of a storm, just two or three hours before. In this way, people
of my village in north Portugal call me " the guy of storms ", because
I predict the storms arrival.
DAY TIME PROPAGATION
In day time, the base of the ionosphere is composed
by the D layer. This layer extend between 70 and 90 km high. This region
is composed by big molecular particles that gives a high wave attenuation.
The atmosphere is composed by a lot of particles and atoms. The ionosphere
is composed principally by free electrons. When this two regions are in
contact, it makes a new region called the D layer. This layer is responsible
of the high attenuation in LF and HF transmission, below 6 Mhz.
 |
|
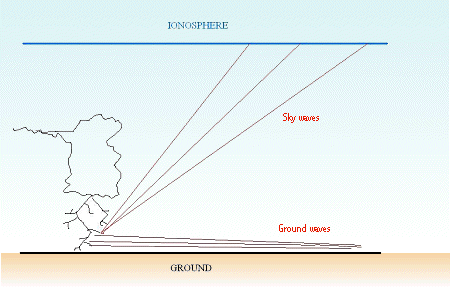
A return stroke, as any kind of radio transmitting
antenna, radiates two types of waves: the ground wave and the sky wave.
The first propagate along the earth ground, the second propagate by reflections
in the ionosphere.
In day time the D layer absorbs all the sky waves
coming from return strokes, so the only one we can receive is the ground
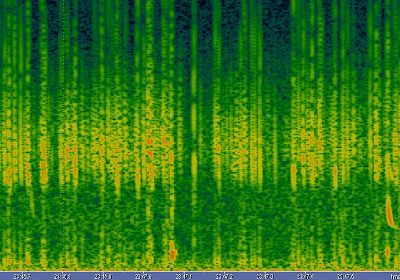
wave, I suppose. This is shown in the picture 1.
Because of the absorption of sky waves, the earth
and the ionosphere doesn't act as a waveguide, I suppose. |
Picture 1: day time propagation
And so the waveguide effect (tweeks) doesn't appeared,
we only heard spheric noise.
NIGHT TIME PROPAGATION
This kind of propagation start to appeared about
2 hours before the sunset, and disappeared at sunrise because of the high
speed recombination of the D layer.
 |
|
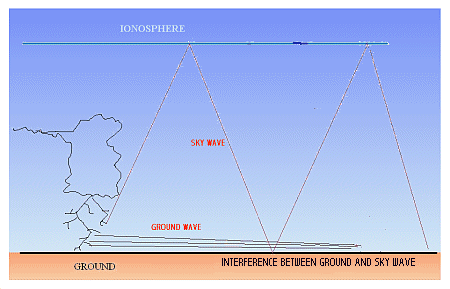
In night time, the D layer disappeared, and so
the base of the ionosphere is composed by the E layer. This layer extend
between 90 and about 150 km. This region is only composed by free electrons,
so this region act as a reflecting layer. Now the sky waves can propagate
by reflections between the earth and the ionosphere, and so the waveguide
mode can appeared, as we see in the picture 2 |
Picture 2: night time waveguide
propagation.
As in HF propagation, interference can appeared
between ground wave and sky wave, in HF this is called " fading " and it's
a really common phenomenon in the Medium Wave broadcasting band.
 |
|
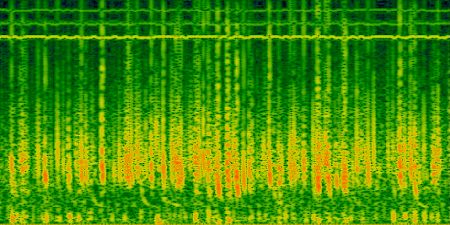
It's in that way I explain the " sudden stop "
of spherics around 3 or 4 Khz, as we see in picture 3.
At night time, the bigger part of the spherics after
a long travel in the earth ionosphere waveguide become tweeks, and I'm
going to explain why. |
Picture 3: " sudden spherics
stop " at around 3 Khz.
All waveguides have a cut off frequency Fc, they
work as a high pass filter. Below Fc, no EM waves can propagate, over Fc
EM waves can propagate with a given speed v.
For a rectangular waveguide Fc is given by:
(1) 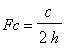
Where: h is the vertical high of the waveguide.
c is the light speed in the vacuum c=299792458 m/s.
They become a dispersing medium for waves with frequencies
near Fc. Dispersing means that all the frequencies don't arrive at the
same time.
In a rectangular waveguide the speed of the wave
is given by :
(2) 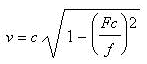
Where: c is the light speed in the vacuum c= 299792458
m/s.
Fc is the cut-off frequency of the wave guide.
 |
|
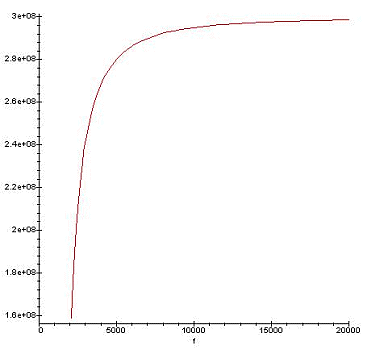
If we look closely to the formula
(2), we can deduce that the wave speed is equal to 0 m/s at Fc and that
the speed grow as the frequency become higher, see picture 4. It's clear
is that which affect the spherics propagation and transform them in to
tweeks.
A tweek as we see them on spectral analyses is first
composed by a vertical part, this is because the frequencies are still
far enough from FMC, and as a result they arrive all at the same time.
About 200 Hz before Fc, all the frequencies don't
arrive at the same time and we see a sort of curve in the spectrum: it's
the begin of the tweek. A tweek theoretically never finish because near
Fc, the speed is so low that the wave will take a very long time to arrive
at the listening place. |
Picture 4: speed wave in
m/s, Fc= 1780 Hz.
Thanks to the formula (2), the simulation of a tweek
is almost easy, if we put v=d/t, where d is the distance between the return
stroke and the listening place and after doing a little calculation we
can have a formula that gives the tweek spectrum for all the distances
value we want, this formula is the next one:
(3) 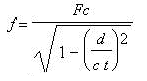
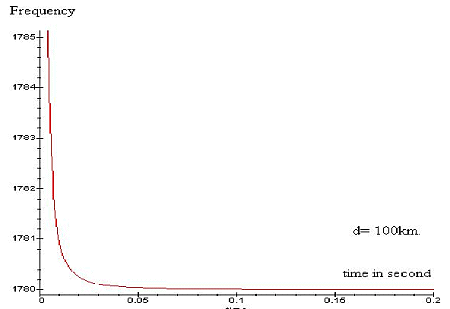
Taking this formula, we can compute it on a computer
or a graphic calculator and extract the tweek spectrum, some examples are
given in picture 5 and 6. We see in the first picture that the dispersion
is low, because d is only 100 km, so we deduce that spherics are signal
which not propagate a lot in the earth-ionosphere waveguide. Instead of
tweeks which are spherics that propagate a lot in the waveguide, in this
case d must be greater than 1000 km.
Picture 5: Fc= 1780
Hz.
Picture 6: Fc= 1780
Hz.
CALCULATION
OF THE DISTANCE BETWEEN THE RETURN STROKE AND THE LISTENING PLACE, THANKS
TO SPECTRAL ANALYSES
This is my favorite topic about tweeks, one year
ago I was looking for information about tweeks, but I founded nothing to
deduce the distance between lightning to the observatory using tweeks spectrum
analyses.
So I started to use my brain, and finally I founded
a really simple formula that I'm going to explain.
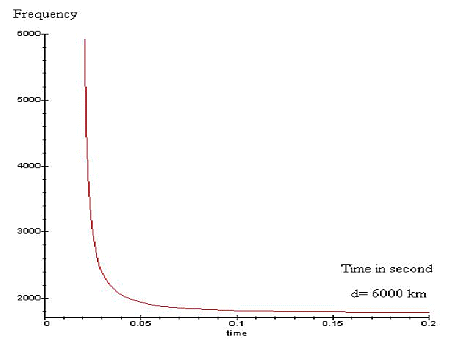
Suppose at a time t=0, a return stroke radiate energy
in
the earth-ionosphere waveguide, now suppose also that the speed wave near
6 Khz is close to c, the light speed. This wave will take a time tc=d/c,
to arrive at the listening place. In the other hand the speed wave v at
an other frequency in the " curve " of the tweek, will take a time tv=d/v,
to arrive at the listening area. But the only time we can measure in spectrum
analyses are the dispersion time between higher and lower frequency, this
time is called dT.
By looking to picture 7, we deduce dT= tv-tc.
 |
|
So we have:
(4) 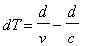
And after a little calculation, we found:
(5) 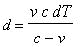 |
Picture 7: using this graph
to deduce distance d.
THEORETICAL
EXAMPLE OF CALCULATION
Let me take again the picture 6, if we measure
the dispersion time dT between a frequency of 6 Khz and a frequency of
2 Khz, we have dT=0,024 s or 24 ms. At 2 Khz the speed wave is 136693526
m/s. Computing this data in formula (5) we found d= 6030 km because I don't
take all the decimal numbers, but the formula works good !
In conclusion, never forget, longer the tweek
is, longer the wave have traveled in the earth-ionosphere waveguide.
PRACTICAL EXAMPLE
OF CALCULATION
With a spectrum analyses we can only have an estimation
of d, not an exact value because of all the precision errors in our computer
spectrum software.
Here we are going to estimate the distance between
my listening place and the return stroke that give the birth to this two
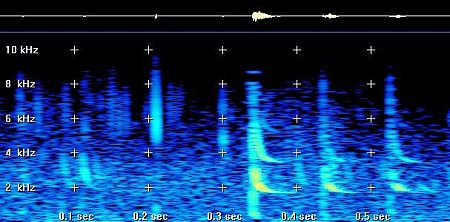
hops whistler, recorded in the 27 December 2002, picture 8.
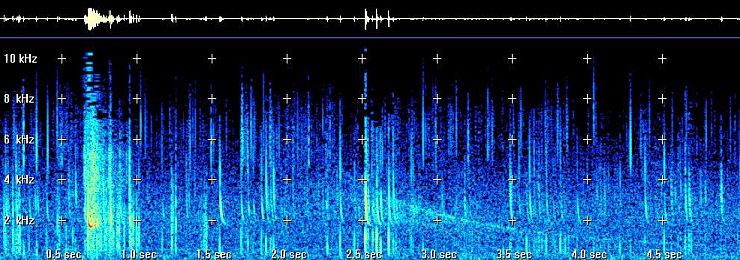
Picture 8: the same
return stroke propagate by the wave guide mode (tweek) and the magneto-ionic
mode (whistler).
By looking to the spectrogram, we have Fc= 1745
Hz, the dispersion time between 6 KHz and 1830 Hz is dT=4 ms. The wave
speed at 1830 Hz is 90306,1 km/s. And with the help of formula (5), we
found d= 517 km. According to the formula the return stroke may be at around
500 km, from CICOURO, my recording place in north Portugal.
DRAGON
TWEEKS, VERY LONG TWEEKS and SHORT TWEEKS
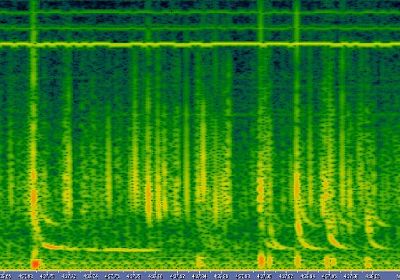
Here you can see a tweek that I called dragon tweek
because it extends really high in frequency. It's a strange one, the 1,3,5...harmonics
order of Fc are stronger than the 2,4,6...harmonics order of Fc, it's still
not explain, see picture 9.
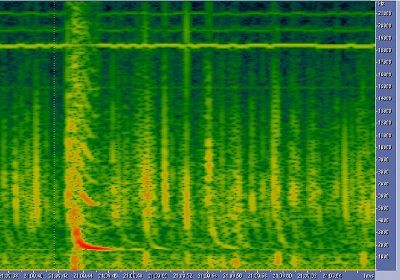 |
|
Sometimes some very long tweeks can appeared, they
are originated from very good " return stroke radiator " and have traveled
over 6000 km in the earth-ionosphere waveguide, their duration in time
can be greater than 150 ms.
Picture 9: Dragon tweek. |
 |
|
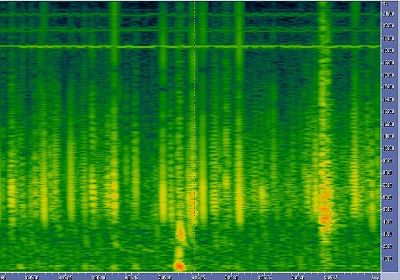
Something appeared strange is that the second order
of Fc is shorter than the first, still not explained.
The 5 others tweeks are originated from the same
lightning, because they are closed in time and have about the same dispersion.
Picture 10: A very
long tweek.
|
 |
|
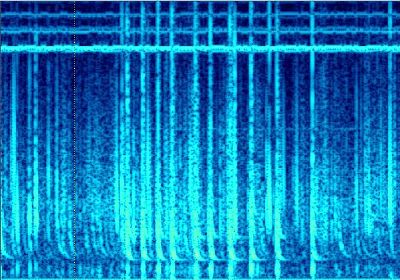
Short tweeks can also be heard, as this one, in
the center of picture. As we know now, they are originated from " near
" storms.
Picture 11: A short
tweek. |
HYBRID TWEEKS
This kind of tweeks are really common and appeared
about all of the time. According to the waveguide theory explained before,
no EM waves can propagate below Fc. But sometimes when tweeks appeared,
a strange vertical part of the tweeks is also visible below Fc, on spectrum
analyses.
 |
|
Tree Japanese scientist (Kohji Kawakita, Takuya
Kawakami, Takeo Yoshino) called this tweeks: hybrid tweeks.
Some hybrid tweeks radiated by the same lightning
received in Portugal are shown in Picture beside.
According to the paper they wrote, typical tweeks
number is greater when geomagnetic activity is high and hybrid tweeks tend
to appeared in quiet days. As a result they show that tweeks propagation
is also affected by geomagnetic activity. |
Picture 12: hybrid tweeks.
 |
|
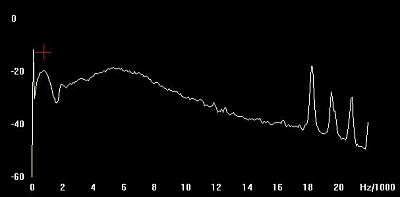
In the picture beside, you see a spectrum analyses
of VLF signals, the reception of signals from hybrid tweeks appeared clearly
with a maximum at about 700 Hz.
The first Fc order is well visible at around 1700
Hz. |
Picture 13: VLF spectrum.
NO PREDICTED
WAVEGUIDE SIGNALS
 |
|
Some signals similar to the lower part of hybrid
tweeks, are still strange for me. It's a kind of spheric that have maximum
below Fc, at around 700 Hz. It sounds as " TOC ", we can see one of them
in the picture 14. The strangest thing, it's the maximum signal at around
700 Hz.
Picture 14: strange
signal below Fc.
|
IONOSPHERIC
HEIGHT REFLECTION
This is an interesting chapter that tell about
the calculation of the reflection height of the waves coming from the return
stroke.
This calculation is really simple using formula
(1) 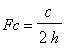 , h
is given by:
, h
is given by:
Cut frequency variations:
(6) 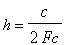
1°) " power wave " variations:
Taking measures of Fc is interesting, sometimes
tweeks (in the same record) don't have the same Fc, according to me, it's
because some waves are more powerful than other and so they can penetrate
a little bit more the ionosphere, as a result, the value h is not the same
and so Fc. For example, some tweeks can have Fc=1700 Hz and others can
have Fc=1820 Hz.
For the first Fc it gives h=88 km and for the second
h=82 km.
2°) sun set and sun rise variations:
At day time the ionospheric height base is about
70 km, in night time as we calculate just before this height is near 90
km. Variations of Fc occurred when the sun go down or up. I never record
it, but it can be interesting to monitor one hour before and after the
sun set or the sun rise.
3°) seasonal variations:
Because of different ionization along the year,
also Fc variations can be seen by doing an average in summer and winter
tweeks reception. In winter time, I measured a cut frequency off 1675 Hz,
it gives h=89 km.
 |
|
To finish I want to show you a little picture of
some tweeks, as they sound, I called them echo tweeks, but we can easily
see that they come from the same lightning, but from different return strokes.
The first tweek have a Fc of 1690 Hz, the second
of 1720 Hz, and the third of 1840 Hz, the different reflection height are
88 km, 87 km, 81 km. |
Picture 15: tree nice tweeks.
This different height of reflection can be explained
by the fact that the lightning loss energy in every return strokes and
so the waves penetrates lower in the ionosphere, I explain it like that.
CONCLUSION
I hope you enjoy reading this paper about tweeks
waves, now when conditions will not so good to receive whistlers, chorus,
hiss, or triggered emissions, you will take interesting time to hear the
TIOUK sound of the tweeks. Other things are to said, sometimes tweeks appeared
or sound strange, now you will have to take a little more care when you
look at your records, look how are the tweeks...
And who will be the listener to record the longer
tweeks never received ?
DEDICATION AND
THANKS
I dedicate this little paper to the memory of my
friend Georges Cacheux (F8CG), one of greatest french ham radio, who sadly
died two years ago of a disastrous disease. As a result, I'm the only one
now taking care of the radio-club F6KEO, when it appended we was together
doing our first step in VLF reception.
So, I want to thanks some people that support me:
Renato Romero (IK1QFK) and Jorgen Mortensen (OZ1MAS), that I contact first
in December 2001, and also Bill Taylor from the INSPIRE project, thanks
to this tree persons I learn more about the world of VLF.
All the members of the yahoo VLF list for the things
they done and the things they will do.
And also to Pascal Broccolichi a french modern artist
who is trying him and his team of students to classify all the VLF sounds.
Also a great thanks to the SATEDU team workers and
their director Ghislain Ruy, me and them we are now trying to put a VLF
receiver in the last french ham radio satellite SATEDU.
To finish, I want to thanks the french ham radios
VLF listeners as for example: Jean-Louis Rault (F6AGR) president of the
AMSAT-France for all the discussions we done about VLF sounds and the great
things he know about the topic, Nicolas (F4DTL), Michel (F5WK), Jean Brunet
and Jean-Marie (F1FHP).
Thierry Alves, portuguese and french VLF listener,
SWL, student in electricity, and member of the radio-club F6KEO.
Contact: Thierry ALVES. e-mail : elf_vlf@hotmail.com
In France at my home:
162, AV PDT R Schuman.
33110, Le BOUSCAT.
In france, at F6KEO ham radio station:
Jeunes Science Bordeaux :
tel. 05.56.85.75.15 from France.
tel. 00.33.5.56.85.75.15 from any other country.
In Portugal:
5210-020 CICOURO.
MIRANDA DO DOURO.
Return to the main
index